(11) 경제학으로 본 저출산 및 고령화 문제

목차

1. 1. 미시적 측면에서 바라본 저출산 및 고령화
   1. 1) 개인의 효용함수
      1. ① 기본가정
      2. ② 저출산 및 고령화에 적용
   2. 2) '생애주기가설' 측면
      1. ① 기본가정
      2. ② 저출산 및 고령화에 적용
2. 2. 거시적 측면에서 바라본 저출산 및 고령화 
   1. 1) 솔로우모형
      1. ① 기본가정
      2. ② 정상상태(Steady State)와 황금률(Golden Rule) 자본수준의 관계
      3. ③ 저출산 및 고령화에 적용

 

최근 저출산 및 고령화가 우리 사회의 화두이자 나라의 근간을 흔드는 문제로 주목받고 있습니다.

 

하긴 출산율이 곧 0.6명 대로 떨어질 것이라는 뉴스도 나오면서 이제 놀랍기 보다는 이러한 추세가 앞으로 우리 삶에 어떻게 영향을 미칠지 걱정이 앞섭니다......

 

한국의 연도별 합계출산율(명) (자료출처: 통계청, 국가통계포털)

 

최근 초등학교에 근무하는 지인들을 만나면서 자신이 "한 반에 12명을 맡는다", "학교 건물의 반은 공실이다", "곧 교사수가 학생수보다 더 많아질 거 같다" 등의 말을 들으면서놀라움과 동시에 우리의 미래에 대한 걱정이 밀려왔습니다......

 

그래서 오늘은 우리나라의 저출산 및 고령화에 대해 다뤄보도록 하겠습니다. (역시나 제 맘대로......^^;;;) 

 

 

1. 미시적 측면에서 바라본 저출산 및 고령화

 

혹자는 이렇게 말씀하실 수도 있습니다.

 

 

"결혼 및 출산의 자유는 개인의 선택이자 자유이고 개인이 책임져야 하는 문제이기 때문에 사회나 국가가 이를 강요해서는 안된다"

 

 

미시경제학적 측면에서 보면 이 말은 맞는 말로 보입니다. 

그럼 왜 그런지 '개인 효용함수'와 '생애주기가설' 등을 통해 분석해보도록 하겠습니다. 

 

 

1) 개인의 효용함수

 

① 기본가정

ㄱ. 효용함수는 개인의 만족감을 수치화한 것이다.

- 효용함수: U(X₁, X₂​,…,Xn​) / U: 효용(Satisfaction 또는 Utility) / X₁, X₂​,…,Xn​ 는 개인이 소비하는 재화 및 서비스

 

ㄴ. 분석의 편의를 위해 개인이 소비하는 재화 및 서비스 X와 Y 두 개뿐이고, 그 가격의 각각 Pₓ, Pᵧ 로 하며 개인의 총 예산은 M이라고 할 때 예산제약식은 M = X · Pₓ + Y · Pᵧ 라고 정의한다.

 

ㄷ. 개인의 효용함수는 콥더글라스 함수로 한정하며,(X, Y 두 재화가 보완재적 관계이다. 이 때 함수형태는 U = Xᵃ · Yᵇ 로 정의한다.( ᵃ + ᵇ = 1 이다.)

- 예를 들어 인터넷 서비스와 넷플릭스의 관계를 들 수 있는데 인터넷 서비스 가격 상승(▲) → 인터넷 서비스 수요 감소(▼) → 넷플릭스 수요 감소(▼)  로 생각할 수 있다.

 

ㄹ. '한계효용체감의 법칙'이 적용된다.

- 쉽게 말해 배가 고파서 햄버거를 1개 먹을 때는 그 만족감이 가장 크지만 2개, 3개 등 계속 먹을수록 배가 부르고 나중에는 배탈이 나면서 오히려 불쾌감만 느는 것을 생각하면 된다.

 

ㅁ. '한계대체율(MRS, Marginal Rate of Substitution)'은 무차별곡선의 기울기(아래 그래프의 예산제약식과 무차별곡선이 접하는 효용극대화점으로써 소비자가 동일한 만족감을 느끼는 재화 간 교환비율을 말한다.

- 말이 매우 어려운데 예를 들어 커피와 설탕이 있을 때 개인이 커피를 일정 부분 포기하면서 설탕을 얼마큼 얻어야 동일한 만족감을 얻는지에 대한 재화 간 교환비율로 생각하시면 됩니다.

- { (커피 100, 설탕 0), (커피 10, 설탕 90), ...... (커피 50, 설탕 50),..... (커피 90, 설탕 10), (커피 100, 설탕 0)} 와 같은 커피와 설탕의 교환비율은 1:1로써,  한계대체율은 커피를 포기하고 설탕을 얻어 동일한 만족을 유지하는 비율로 이해하면 됩니다.

- MRS = - (∂Y / ∂X) = (∂U / ∂X) / (∂U / ∂Y) 로 정의되는데 여기서 (-) 기호가 붙은 이유는 한 재화를 포기할 때를 의미합니다.

 

 

ㅂ. 개인의 목표는 만족감을 최대로 느끼는 것이다.

 

Max U(x,y) = Xᵃ · Yᵇ  subject to  X · Pₓ + Y · Pᵧ ≤ M

 

ㅅ. 예를 들어 다음과 같이 그래프로 나타내면,

빨간선은 예산제약선 그리고 파란곡선은 무차별곡선입니다. 현재 이 사람은 X, Y재화를 각각 50개씩 소비했으며, 이때 만족감을 50으로 느끼고 있는 상태입니다.

 

 

M = 50 ½  · 50 ½  => max U = 50라고 정의할 수 있으며, 이를 해석하면 한 개인이 X재화를 50개, Y재화를 50개 소비했을 때 만족감 U가 50이 되고 이는 개인의 예산제약하에서 최대의 만족감 효용을 느끼는 상태를 의미한다. 

 

 

이렇게 복잡한 정의를 소개하면서 말하고자 하는 내용은 다음과 같습니다.

 

 

② 저출산 및 고령화에 적용

ㄱ. 최근 '출산' 및 '아기'는 '최고의 사치재'라는 매우 자극적인 표현이 유행하고 있습니다.

 

ㄴ. 아이를 출산 및 육아하는 것을 하나의 재화 또는 서비스라고 가정해봅시다. 이 경우, 개인이 출산 및 육아를 선택할 때 포기해야 하는 여가와 소비활동(다른 재화 및 서비스)의 교환비율(한계대체율)이 높다고 볼 수 있습니다. 

→ 즉, 한계대체율(MRS, Marginal Rate of Substitution)이 높다는 것은, 출산 및 육아를 1단위 추가로 선택할 때 포기해야 하는 여가와 소비의 양이 매우 크다는 뜻입니다.

→ 쉽게 말해 딩크족으로 살면 훨씬 더 많은 여가와 소비활동을 할 수 있기 때문에, 여가와 소비에 비해 출산 및 육아가 선택되기 어려운 상황임을 설명할 수 있습니다.

 

ㄷ. 어떤 개인에게 출산 및 육아라는 선택은 예산제약 내에서 소비할 수 없는 사치재처럼 보일 수 있습니다. 이는 개인의 예산제약선을 넘어선 소비 지점에 해당하며, 이 경우 출산 및 육아는 선택지에서 제외됩니다. 

→ 아이를 갖는 데 드는 비용(금전적, 시간적, 심리적)이 지나치게 커, 여가와 소비를 포기하면서까지 선택할 수 없는 구조를 의미합니다.

 

ㄹ. 이를 현실에 적용하면, 한 가정에서 벌어들이는 수익(예산, M)에 한계가 있으면 출산 및 육아라는 재화(또는 서비스)는 너무 비싸서 소비가 불가능하며, 소비가 가능하더라도 출산을 포기하고 다른 재화 및 서비스를 소비하는 것이 개인에게 더 큰 효용을 줄 수 있다 해석할 수 있습니다.

 

ㅁ. 이럴 경우 앞으로 개인 및 가정의 소득이 증가(▲)하거나 정부의 각종 지원으로 재화 및 서비스의 가격이 감소(▼)하거나 재화 및 서비스를 무상으로 지원받을 경우에 결혼 및 출산이 증가할 수 있을 것입니다.

 

 

결국, 저출산의 문제를 개인에게 맡길 경우 해결하기 어려우며, 사회 구조적인 문제로 바라보고 접근해야 한다는 결론을 내릴 수 있습니다.  

 

 

2) '생애주기가설' 측면

 

(좌측) 초기 부(현재 자산)을 고려하지 않은 단순화한 생애주기가설 그래프, (우측) 생애주기가설 식 정리

 

① 기본가정

ㄱ. 사람들은 일정한 소비 수준을 유지하려고 한다.(소비 평탄화, Consumption Smoothing)

 

ㄴ. 취업 전에는 소득이 없어서 대출(S₂)을 통해 생활하다가(청년기), 취업 후 소득이 점진적으로 증가하면서 저축(S₁)을 하게 되고, 은퇴 후 축적된 저축을 소비(S₃)하게 된다. (S₁ = S₂ + S₃)

 

ㄷ. 개인은 자신의 생애 동안 발생할 총소득을 정확히 에측하고 이에 맞춰 소비 및 지출을 한다. (현실적으로 이런 사람은 거의 없겠죠?! 그냥 이론을 위한 전제로 받아들여 주세요!)

 

ㄹ. 분석의 편의를 위해 세대 간 '유산'을 주고 받지 않으며, 필요할 때 대출을 받을 수 있다.(차입제약이 없다.)

 

② 저출산 및 고령화에 적용

ㄱ. 의학기술의 발전에 따른 기대수명의 증가로 은퇴 이후의 소비(S₃) 수준 또한 증가하게 될 것입니다.

※ 의학기술 발전 → 수명증가 → 은퇴 후 생활비 증가(S₃)  

 

ㄴ. 이는 취업 후 은퇴시점까지 축적한 저축( S₁) 수준이 크게 변하지 않는다면(현재 우리의 실질소득의 증감율을 보면 오히려 감소 중이죠......), '소비 평탄화'를 고려할 때 결혼 및 출산에 따른 비용을 지출하는 것에 부담을 느끼게 될 것입니다. 

 

ㄷ. 즉, 결혼 및 출산의 감소가 이어져 저출산이 예상되며, 개인 수명의 증가는 소비 평탄화 수준(평생의 일정한 소비수준) 또한 낮출 것입니다.

 

ㄹ. 결국, 소비 침체에 따른 내수 위축, 노인부양인구 증가에 따른 노동력 부족 및 노인복지비용 증가 등이 유발될 것입니다.

 

 

이론의 가정이 현실에 100%로 부합되진 않지만, 일본 및 우리나라의 현 상황을 해석하는데 도움이 된다고 생각되는데 여러분은 어떻게 생각하시나요?

 

 

2. 거시적 측면에서 바라본 저출산 및 고령화 

 

 

그러면 이제 거시경제학적 측면에서 저출산 및 고령화를 바라보도록 하겠습니다.

 

 

1) 솔로우모형

 

① 기본가정

ㄱ. '자본 축적', '노동력 증가', '기술진보'가 경제성장에 영향을 주는 요소이다.

 

ㄴ. 생산(Y)는 자본(K), 노동(L), 기술(A)에 의해 결정되며, Y = F(L, K, A) 로 정의할 수 있다.

※ 편의를 위해 Y는 GDP, K는 설비기계, L은 노동인구, A는 AI와 같은 기술 수준이라고 생각하면 쉽겠죠?!

 

ㄷ. 콥더글라스 생산함수를 다음과 같이 적용하자.

- Y = Kᵃ · AL¹⁻ ᵃ  ,  0 < a < 1 / a: 자본의 생산성 기여도

 

ㄹ. 규모수익불변(CRS, Constant Returns to Scale)을 가정한다.

- 생산요소를 동일 비율로 증가시키면 생산량도 동일 비율로 증가함을 의미한다.(F(cK, cL) = c⋅F(K, L))

 

ㅁ. 기술진보율(g)과 인구증가율(n)은 외생요소이다.

→ 쉽게 생각하면 단기적으로 반도체 공장에서 고용을 늘리고 최신 생산 기술을 도입하더라도 생산량의 증가가 제한적일 수 있지만, 장기적으로 생산의 효율성이 개선되어 총생산량이 크게 증가하게 된다고 이해하면 좋을 거 같습니다. 

 

ㅂ. 자본(K)은 감가상각률(δ) 그리고 노동은 인구증가율(n)에 영향을 받는다.

 

ㅅ. 소득의 일정 부분은 저축률 s만큼 저축되고(sY), 이는 투자로 이어진다.(I = sY)

 

ㅇ. 자본축적 방정식은 다음과 같다.

- △K = sY - (δ + n) · K,   △K: 자본량 변화, sY: 투자, (δ + n) · K : 감가상각 및 인구증가에 따른 자본 감소

 

ㅈ. 정상상태(Steady State, k*): 경제가 더 이상 자본 축적(자본량 증가나 감소)을 경험하지 않는 균형 상태를 말하며, sF(k) = (δ+n)k, k = K / L 로 1인당 자본량(자본집약도) 로 정의할 수 있다.

 

ㅊ. 1인당 생산함수는 y = f(k) = F( K / L,1), y = Y/L, k = K / L 로 정의할 수 있다.

 

ㅌ. 기술진보는 생산함수의 위치를 위로 이동시켜 장기적으로 경제성장을 촉진시킨다.

 

ㅍ. 그래프를 통해 앞에서 언급한 가정을 정리하면,

 

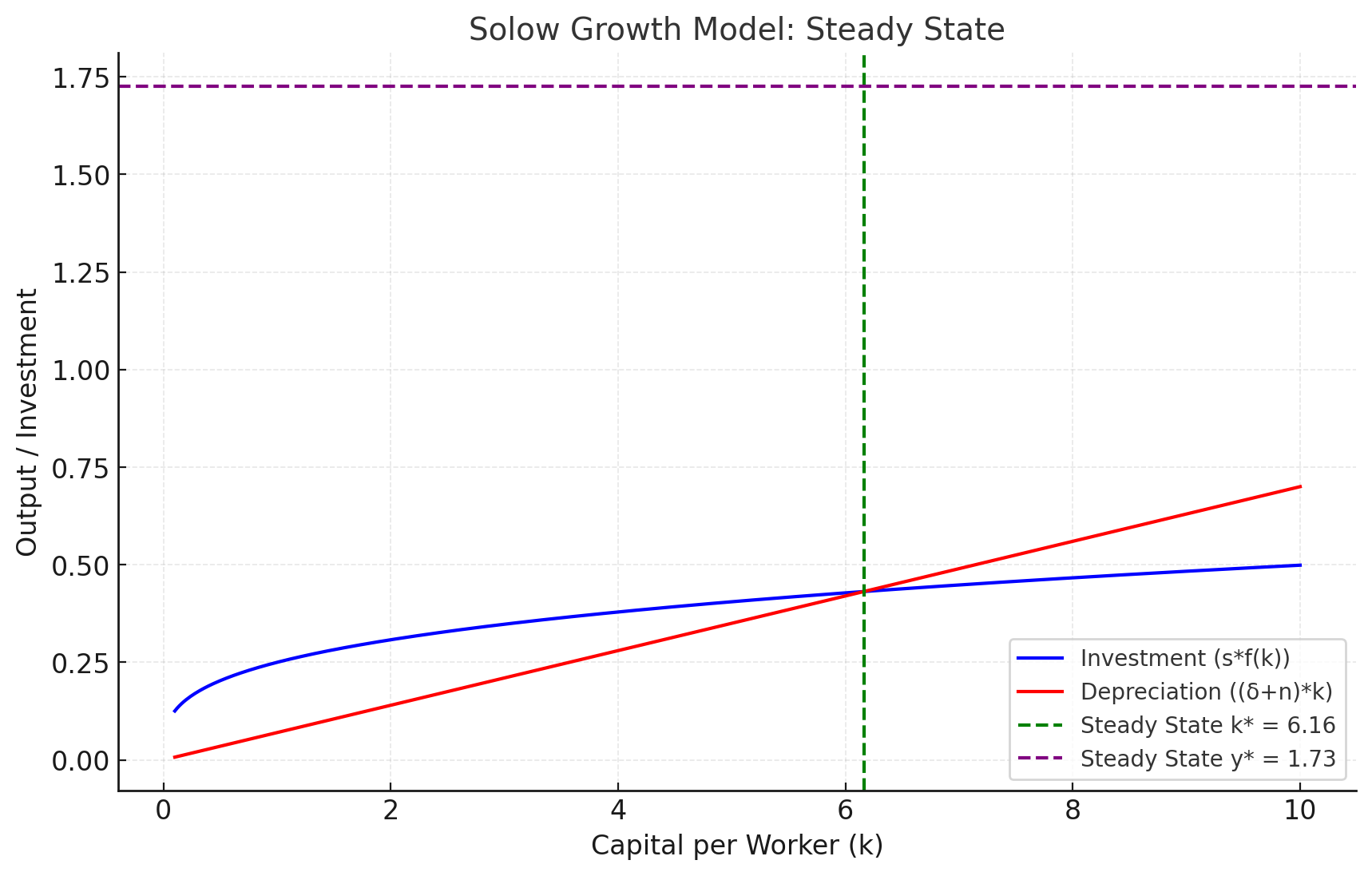
솔로우 모형의 예시와 솔로우 모형 수식 정리

 

 

- 파란색 곡선은 저축률(s)에 따른 1인당 자본량에서의 투자를 말한다.(s⋅f(k))

- 빨간색 곡선은 감가상각률(δ)과 인구증가율(n)에 의해 감소하는 자본량을 말한다.

→ 예를 들어 기계·설비를 사용할수록 그리고 시간이 지남에 따라 감가상각이 일어나 자본량이 감소하게 되며, 인구 증가에 의해 노동력(L)이 늘어 고용이 확대될 경우 1인당 사용할 수 있는 기계·설비의 양(1인당 자본의 양)이 줄어들게 됩니다.

- 녹색 점선: 정상상태(Steady State)의 1인당 자본량(k*)를 의미합니다.

- 보라색 점선: 정상상태(Steady State) 의 1인당 생산량(y*)를 의미합니다.

 

이를 정리하면, y* = f(k*),  s ⋅ f(k*) = (δ+n) ⋅ k*,  k* = (s / (δ + n))^(1 / (1 - α)), α: 생산함수 f(k) = k^ α 의 자본 기여도로 정리할 수 있습니다.(솔직히 경제학 전공자 아니면 이해하기 빡시긴 합니다...^^;;;)

 

ㅎ. 정상상태(Steady State)에서 반드시 최적자본수준(황금률)을 달성하지 못한다. 

- 최적자본수준(k*)은 한 경제에서 '1인당 소비를 극대화'하는 '자본 수준'을 의미하며, 이를 '황금률(Golden Rule) 수준'이라고 한다.

- 최적자본수준은 다음 조건에서 성립한다.

→ f'(k)의 의미는 f(k)를 미분한 값으로 1인당 자본수준의 한계생산성(MPk)를 의미함

→ f'(k_gold) = δ + n, f(k_gold)를 미분한 값으로 1인당 황금률 자본수준의 한계생산성(MPk_gold)를 의미함  

→ MPk(Marginal Product of Capital per Worker)

-  즉, 황금률 자본수준에서 1인당 자본의 한계생산성(MPk_gold)은 감가상각률(δ)과 인구증가율(n)의 합과 같다는 것을 의미함

- 최적자본수준에서 소비가 최대화(c_gold)되며, 이는 반드시 정상상태의 1인당 자본수준(k*)과 일치하지 않을 수 있다.

 

(좌측 그래프) 솔로우 모형의 정상상태(Steady State)와 황금률(Golden Rule) 비교, (우측) 최적자본수준(k*)와 1인당 소비 극대화 관련 정리

 

- 위의 솔로우 모형의 정상상태(Steady State)와 황금률(Golden Rule)에 대한 그래프를 분석하면,

→ 파란 곡선(Investment(Saving Rate)은 1인당 저축률(s)에 따라 계산된 1인당 투자량(s·f(k)) 입니다.

→ 정상상태(Steady State)에서 이 곡선이 빨간 점선(δ + n)과 교차하는 지점에서 자본량이 균형을 이룹니다.

→ 초록 점선(Investment(Golden Rule Saving Rate)은 황금률 저축률(s_gold) 따라 계산된 1인당 투자량(s_gold·f(k))을 나타냅니다.

→ 황금률 자본수준(k*_gold)에서는 이 곡선 빨간 점선(δ + n)과 교차합니다.

→ 빨간 점선(Depreciation(δ) + Population Growth(n))은 (δ + n)·k로 감가상각률(δ)과 인구증가율(n)에 따른 1인당 자본 감소량을 나타내며, 자본 축적 과정에서 소모되는 자본량을 설명합니다.(자본량에 비례하는 증가함수)

→ 보라색 세로선(Steady State Capital)은 파란 곡선(저축률 투자 곡선)과 빨간 점선(자본 감소율 점선)이 교차하는 지점으로 자본량(k*_steady)은 일정하며, 더 이상 증가하거나 감소하지 않는 정상상태 자본수준을 나타냅니다.

※ 정상상태는 현재 저축률에 따라 경제가 균형을 이루는 상태입니다.

 

→ 주황색 세로선(Golden Rule Capital)은 초록 점선(황금률 투자 점선)과 빨간 점선(자본 감소율 점선)이 교차하는 지점으로 이 지점에서 1인당 소비가 최대화됩니다. (c* = f(k*) - (δ + n)·k*) 즉, 황금률 자본 수준으로 자본 축적이 사회적으로 최적화된 상태를 나타냅니다.

 

② 정상상태(Steady State)와 황금률(Golden Rule) 자본수준의 관계

ㄱ. 만약 정책적으로 저축률 s가 조정되지 않은 상태라면 정상상태 자본량(k*)는 주어진 s에서 도출되며, 이는 황금률 자본수준 k_gold 와 다를 수 있습니다.

 

ㄴ. 따라서 다음과 같이 정리할 수 있습니다.

 

정상상태와 황금률 자본수준의 관계

 

 

ㄷ. 정상상태는 경제가 내재적으로 도달하는 자본수준일 뿐 사회적 후생(소비 극대화) 관점에서 최적이 아닐 수 있습니다.

 

ㄹ. 정책적 개입을 통해 저축률(s)를 조정하여 정상상태를 황금률 자본 수준으로 이동시킬 수 있습니다.

→ s를 증가시키면 자본축적이 늘어나 k*를 증가시킴

→ s를 감소시키면 자본축적이 줄어들어 k*가 감소됨

 

ㅁ. 정리하면,

→ 정상상태는 경제가 자본 축적이나 감소 없이 균형을 이루는 상태일 뿐이다.

→ '최적자본수준(황금률 수준)'은 '소비를 극대화'하는 자본 수준으로 정책적 조정을 통해 정상상태를 최적자본수준으로 이동시킬 수 있다.

→ '정상상태'는 '현재 경제의 자본축적이 멈춘 균형점'으로 해석하고, '최적자본수준'은 '사회적 후생이 극대화되는 자본량'으로 구분하는 것이 바람직하다. 

 

 

③ 저출산 및 고령화에 적용

위의 솔로우 모형을 저출산 및 고령화에 적용하면,

 

 

(1) 노동인구(L)의 감소

 

ㄱ. 저출산은 인구 감소를 유발하여 일할 사람이 부족하게 됩니다.(L 감소)

 

ㄴ. 1인당 자본량(MPk)이 증가할 수 있으나 '한계생산체감의 법칙(Diminishing Marginal Product)'에 따라 경제 전반에 제한적인 영향을 미치게 됩니다.

→ 쉽게 말해 아르바이트로 햄버거 가게에서 햄버거를 만들 때 개인이 활용할 수 있는 주방기기가 늘어나는 것을 의미하는데 개인의 피지컬에 한계가 있기 때문에 나중에 아무리 주방기기를 늘려도 생산이 늘지 않는다고 생각하시면 됩니다.

 

ㄷ. 즉, 개인의 생산량은 늘더라도 사회 전반의 생산량(GDP)은 감소할 가능성이 큽니다.

→ 개인이 활용할 수 있는 기계 및 설비가 늘어날 수 있겠지만, 사회 전체적으로 저출산에 따른 노동력 감소는 노는 기계 및 설비(유휴설비)를 늘려 총생산량을 감소시킬 것입니다.

 

ㄹ. 물론, AI와 같은 기술진보(g) 및 기술 수준(A)의 발전으로 인해 한계생산체감의 법칙이 적용되지 않을 경우 인구의 감소로 인한 총생산량의 감소는 어느 정도 상쇄될 수 있겠지만, 그 때가 언제일까요? ㅜㅜ

 

 

(2) 저축 및 투자의 감소

 

ㄱ. 생애주기가설에서 다루었듯이 고령층은 중년층까지 축적한 자산을 소비하는데 사용하기 때문에 사회 전체적인 저축률(s)이 감소할 것으로 예상됩니다. 

→ 우리 주변 할아버지, 할머니들이 경제활동을 통해 저축을 하는 경우가 얼마큼 될지 생각해 보면 쉽게 이해되시죠?!

 

ㄴ. 이는 저축 감소(▼) → 투자 감소(▼) → 자본 축적 수준 감소(▼) → GDP 감소(▼)로 이어지게 됩니다.

 

ㄷ. 기술진보(g)와 기술 수준(A)의 발전과 관계없이 자본(K)의 감소로 경제 성장이 정체될 것으로 예상됩니다.

→ 예를 들어 획기적인 AI 기술이 개발되었더라도 이 기술을 도입할 기계 및 설비가 부족할 경우 결국 생산량이 감소하게 된다고 생각하면 될 거 같습니다.

 

 

(3) 기술 진보(g) 및 기술 수준(A)의 발전

 

ㄱ. 앞서 언급했듯이 저출산에 따른 인구 감소와 고령화로 인한 자본 감소는 총생산량 감소를 초래하여 경제를 위축시킬 가능성이 큽니다.

 

ㄴ. 그러나 기술 진보(g)와 기술 수준(A)의 발전은 이러한 문제를 상당 부분 상쇄할 수 있을 것입니다.→ 예를 들어, AI 기술의 발전은 업무 효율성을 크게 개선시켜 개인의 생산성을 극대화할 뿐 아니라, 업무 프로세스를 간소화시켜 고령층의 노동 참여를 촉진할 가능성도 있습니다.

 

ㄷ. 단, 기술 진보(g)와 기술 수준(A) 발전의 효과는 그 속도와 사회적 수용성에 달려 있을 것입니다. 기술이 도입되기 위해서는 사회 구성원들이 쉽게 이를 수용할 수 있는 사회적 분위기가 조성되어야 하며, 이러한 요인이 충족될 때 총생산량 증가에 긍정적인 영향을 미칠 수 있다고 생각합니다.

ㄹ. 이를 위해 정부, 기업, 대학 등에서 R&D 관련 예산과 제도적 지원을 지속적으로 확대해야 한다고 생각합니다.

 

 

(4) 대응방안 

 

이를 통해 알 수 있는 사실은 저출산 및 고령화 등의 인구문제는 사회 구조적인 문제이기 때문에 다음과 같은 방향으로 대응해야 한다고 생각합니다.

 

ㄱ. 기술 진보(g)와 기술 수준(A) 발전을 위한 R&D 예산 확대와 과학자 및 기술자의 처우 개선

→ 우수 인재 유출 방지: 우리나라 우수 인재들이 해외로 유출되지 않도록 처우를 개선하고, 과학 및 기술 분야에서의 전문 인력이 국내에서 역량을 발휘할 수 있는 환경을 조성해야 합니다.

→ 인재 편중 현상 완화: 우수한 학생들이 특정 직업군(예: 의대)에만 몰리지 않도록 다양한 분야에 대한 사회적 가치와 중요성을 부각시키는 캠페인과 정책이 필요합니다.

 

ㄴ. 최신 기술 습득을 위한 교육 인프라 구축 

→ 교육 지원 제도 점검 및 개선: 나라배움카드와 같은 기존 제도를 점검하고, 디지털 및 첨단 기술 중심의 직업 교육을 강화하여 국민 누구나 새로운 기술을 쉽게 배울 수 있는 기회를 제공해야 합니다. 

→ 취약계층 대상 지원 확대: 저소득층 및 지방 거주민 등 교육 사각지대에 있는 국민들을 대상으로 맞춤형 교육 프로그램과 지원을 확대해야 합니다.

 

ㄷ. 결혼 및 출산 확대를 위한 지원 강화

→ 실효성 있는 정책 수립: 신혼부부, 육아 중인 가정 등의 실질적 수요를 반영한 정책을 마련하고, 직접적인 주거비 지원, 양육비 경감, 공공보육 시설 확충 등 실효성 있는 지원 방안을 강화해야 합니다. 

→ 사회적 공감대 형성: 결혼 및 출산을 장려하는 사회적 분위기를 조성하고, 젊은 세대가 부담을 느끼지 않고 결혼과 출산을 선택할 수 있는 환경을 만들어야 합니다.

 

ㄹ. 고령인구의 경제활동 참여 확대 

→ 고령층 직업교육 지원: 기대수명 증가에 따라 고령층이 경제활동에 참여할 수 있도록 직업교육을 강화하고, 재취업 기회를 확대해야 합니다

→ 사회적 인식 개선: 고령층을 단순한 부양 대상으로 보지 않고, 경험과 능력을 살릴 수 있는 노동인구로 바라보는 인식 전환이 필요합니다.

 

ㅁ. 적극적인 이민 정책 활용 

→ 전문 인력 중심 유치: 전문 기술 인력을 우선적으로 유치하되, 그들의 안정적 정착을 위한 지원책을 마련해야 합니다. 

→ 사회 통합 방안 마련: 이민자와 국민 간의 상호 이해와 협력을 촉진할 수 있는 사회 통합 프로그램을 운영하고, 다문화 사회에 대한 인식을 개선할 필요가 있습니다.

 

 

 

오늘은 경제학을 바탕으로 저출산 및 고령화를 다루어 보았습니다.

 

예전에 공부했던 내용을 정리하면서 다시 한번 해당 문제가 얼마나 우리 삶과 사회에 영향을 미치는지 다양한 각도로 바라볼 수 있었고, 다음에는 이러한 경제이론 이외에 다른 측면에서 저출산 및 고령화를 다룰 수 있도록 하겠습니다.

 

그리고 혹시나 제 개인적인 분석 및 의견에 대해 말씀주실 사항이 있으면 댓글로 달아주시길 요청드립니다!

 

 

 

오늘도 길고 복잡하고 어려운 글 읽어주셔서 대단히 감사드립니다~